RSA算法原理&代码实现
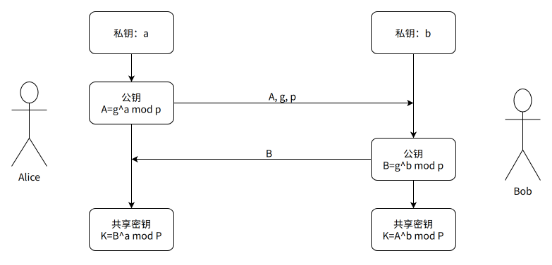
RSA算法原理
数论基础
质数
质数也称素数,是指在一个大于1的自然数中,除了1和此自然数本身,不能被其他自然数整除的数。
模运算
模(Mod)运算即为求余运算。同余是指两个整数除以同一个正整数,得相同余数。
两个整数a,b,若它们除以正整数m所得的余数相等,则称a,b对于模m同余,记作: a ≡ b \ (mod m);读作:a同余于b模m,或者,a与b关于模m同余。例如:26 ≡ 14 \(mod 12)
互质关系
如果两个正整数,除了1以外,没有其他公因子,我们就称这两个数是互质关系(coprime)。比如,15和32没有公因子,所以它们是互质关系。
不是质数也可以构成互质关系。
互质关系的常用结论:
- 任意两个质数构成互质关系,比如13和61.
- 一个数是质数,另一个数只要不是前者的倍数,两者就构成互质关系,比如3和10.
- 如果两个数之中,较大的那个数是质数,则两者构成互质关系,比如97和57.
- 1和任意的一个自然数都是互质关系,比如1和99
- p是大于1的整数,则p和p-1构成互质关系,比如57和56
- p是大于1的奇数,则p和p-2构成互质关系,比如17和15;结合第五条,奇数也是整数,因此,若p是大于1的奇数,则p和p-1、p-2都构成互质关系,比如17、16、15
欧拉函数
欧拉函数𝜑(𝑛)是小于等于n的正整数中与n互质的数的数目。
例如𝜑(8)=4,因为1、3、5和7均与8互质。
计算方法:
- 第一种情况
如果n=1,则 φ(1) = 1 。因为1与任何数(包括自身)都构成互质关系。
- 第二种情况
如果n是质数,则 φ(n)=n-1。因为质数与小于它的每一个数,都构成互质关系。比如5与1、2、3、4都构成互质关系。
- 第三种情况
如果n是质数的某一个次方,即 n = p^k (p为质数,k为大于等于1的整数),则
φ(n) = φ(p^k) = p^k - p^(k-1)
比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 - 4 = 4。
这是因为只有当一个数不包含质数p,才可能与n互质。而包含质数p的数一共有p^(k-1)个,即1×p、2×p、3×p、…、p^(k-1)×p,把他们去除,剩下的就是与n互质的数。
可以写成如下形式:
φ(n) = φ(p^k) = p^k - p^(k-1)= p^k(1-1/p)
若k=1,则是第二种情况
- 第四种情况
如果n可以分解成两个互质的整数之积,
n = p1 × p2
则
φ(n) = φ(p1p2) = φ(p1)φ(p2)
即积的欧拉函数等于各个因子的欧拉函数之积。比如,φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。
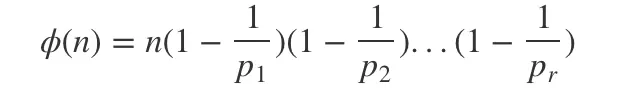
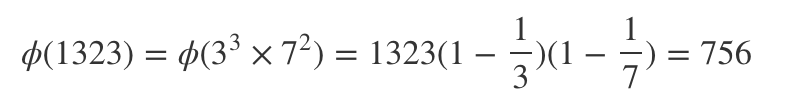
- 第五种情况
任意一个大于1的正整数,都可以写成一系列质数的积。
n = (p1^k1)(p1^k1)...(pr^kr)
根据第四条结论
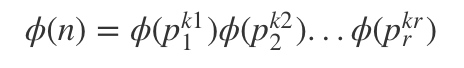
根据第三条结论
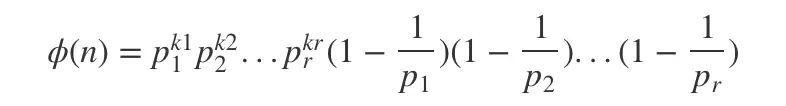
即
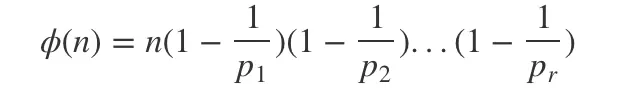
例如
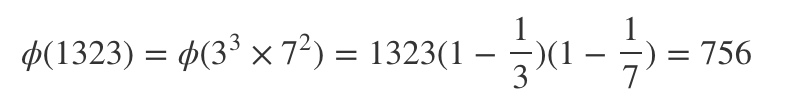
欧拉定理
欧拉函数的用处,在于欧拉定理。
如果两个正整数a和n互质,则n的欧拉函数 φ(n) 可以让下面的等式成立:
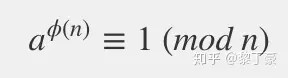
a的φ(n)次方被n除的余数为1。或者说,a的φ(n)次方减去1,可以被n整除。比如,3和7互质,而7的欧拉函数φ(7)等于6,所以3的6次方(729)减去1,可以被7整除(728/7=104)。
欧拉定理可以大大简化某些运算。比如,7和10互质,根据欧拉定理,
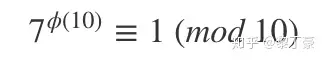
已知 φ(10) 等于4,所以马上得到7的4倍数次方的个位数肯定是1。
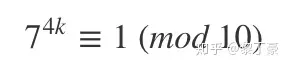
因此,7的任意次方的个位数(例如7的222次方),心算就可以算出来。
费马小定理:
假设正整数a与质数p互质,因为质数p的φ(p)等于p-1,则欧拉定理可以写成
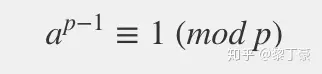
模反元素
如果两个正整数a和n互质,那么一定可以找到整数b,使得ab-1被n整除,或者说ab被n除的余数是1。
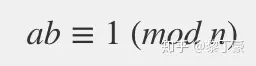
b即为a的模反元素
如:3和11互质,那么3的模反元素就是4,因为 (3 × 4)-1 可以被11整除。模反元素不止一个。

可以看到,a的 φ(n)-1次方,就是a的模反元素。
RSA算法
密钥生成
1.随机选择两个不相等的质数p和q
假设选择了61和53。实际应用中,这两个质数越大,越难破解。
2.计算p和q的乘积n
n = 61 * 53 = 3233= (110010100001)B
n的长度就是密钥长度。
此例中密钥长度为12位,实际应用中,一般为1024位或者2048位。
3. 计算n的欧拉函数φ(n)
n是质数,则 φ(n)=n-1
n = p1 × p2
φ(n) = φ(p1p2) = φ(p1)φ(p2)
=> φ(n) = (p-1)(q-1)
φ(3233) = 60×52 = 3120
4.随机选择一个整数e,条件是1<e<φ(n),且φ(n)互质
这里随机选择17.
实际中,常常选择65537.
5.计算e对于φ(n)的模反元素d
模反元素就是指有一个整数d,可以使得ed被φ(n)除的余数位1
ed ≡ 1 (mod φ(n))
等价于
ed - 1 = kφ(n)
实质上就是对下面这个二元一次方程求解。(-k = y)
ex + φ(n)y = 1
已知 e=17, φ(n)=3120,
17x + 3120y = 1
其中一组整数解为 (x,y)=(2753,-15)即 d=2753
6. 将n和e封装成公钥,n和d封装成私钥
n=3233,e=17,d=2753,所以公钥就是 (3233,17),私钥就是(3233, 2753)。
实际应用中,公钥和私钥的数据都采用ASN.1格式表达。
RSA算法的可靠性
在密钥生成过程中,一共出现了六个数字:p、q、n、φ(n)、e、d
这六个数字之中,公钥用到了两个(n和e),其余四个数字都是不公开的。其中最关键的是d,因为n和d组成了私钥,一旦d泄漏,就等于私钥泄漏。
那么,有无可能在已知n和e的情况下,推导出d?
(1)ed≡1 (mod φ(n))。只有知道e和φ(n),才能算出d。
(2)φ(n)=(p-1)(q-1)。只有知道p和q,才能算出φ(n)。
(3)n=pq。只有将n因数分解,才能算出p和q。
结论:如果n可以被因数分解,d就可以算出,也就意味着私钥被破解
大整数的因数分解,是一件非常困难的事情。目前,除了暴力破解,还没有发现别的有效方法。
RSA算法的加密和解密
加密使用公钥(n,e)
假设要加密的信息为m=65(m必须是整数,且m必须小于n)
解出如下密文c
me ≡ c (mod n)
公钥是 (3233, 17),m=65
65^17 ≡ 2790 (mod 3233)
解的c=2790
解密使用私钥(n,d)
私钥(3233, 2753),c为2790
cd ≡ m (mod n)
即c的d次方除以n的余数为m
2790^2753 ≡ 65 (mod 3233)
解的m=65
代码实现
生成密钥对
from Crypto import Random
from Crypto.PublicKey import RSA
# 伪随机数生成器
random_generator = Random.new().read
# rsa算法生成实例
rsa = RSA.generate(1024, random_generator)
# 私钥的生成
private_pem = rsa.exportKey()
with open("private.pem", "wb") as f:
f.write(private_pem)
# 公钥的生成
public_pem = rsa.publickey().exportKey()
with open("public.pem", "wb") as f:
f.write(public_pem)加密
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5
import base64
# 加密
message = "Hello World!"
rsakey = RSA.importKey(open("public.pem").read())
cipher = Cipher_pkcs1_v1_5.new(rsakey) #创建用于执行pkcs1_v1_5加密或解密的密码
cipher_text = base64.b64encode(cipher.encrypt(message.encode('utf-8')))
print(cipher_text.decode('utf-8'))这里每次使用公钥加密后的结果都不一致,跟对数据的padding即填充有关。
解密
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5
import base64
# 解密
cipher_text = ""
encrypt_text = cipher_text.encode('utf-8')
rsakey = RSA.importKey(open("private.pem").read())
cipher = Cipher_pkcs1_v1_5.new(rsakey) #创建用于执行pkcs1_v1_5加密或解密的密码
text = cipher.decrypt(base64.b64decode(encrypt_text), "解密失败")
print(text.decode('utf-8'))签名
from Crypto.PublicKey import RSA
from Crypto.Signature import PKCS1_v1_5 as Signature_pkcs1_v1_5
from Crypto.Hash import SHA
import base64
#加签
message = "Hello World!"
rsakey = RSA.importKey(open("private.pem").read())
signer = Signature_pkcs1_v1_5.new(rsakey)
digest = SHA.new()
digest.update(message.encode("utf-8"))
sign = signer.sign(digest)
signature = base64.b64encode(sign)
print(signature.decode('utf-8'))使用私钥加签,每次签名是一致的
验证签名
from Crypto.PublicKey import RSA
from Crypto.Signature import PKCS1_v1_5 as Signature_pkcs1_v1_5
from Crypto.Hash import SHA
import base64
#验签
message_verify = "Hello World!"
signature = ""
rsakey = RSA.importKey(open("public.pem").read())
verifier = Signature_pkcs1_v1_5.new(rsakey)
hsmsg = SHA.new()
hsmsg.update(message_verify.encode("utf-8"))
is_verify = verifier.verify(hsmsg, base64.b64decode(signature))
print(is_verify)参考资料:




空空如也!