背景知识

Embeddings

Embedding（嵌入）是拓扑学里面的词。

在深度学习中的意思是使用低纬度的的数据表示高纬度的数据。例如，在NLP中，“ I have an apple ”这句话中的每个单词可以分别用4维向量表示。

I [1,0,0,0]

have [0,1,0,0]

an [0,0,1,0]

apple [0,0,0,1]

这种方法叫做word embedding.

One-Hot编码

one-hot编码是将文本转化成二级制的一种编码。在训练word2vec模型之前，我们需要利用训练数据构建自己的词汇表，在对词汇表进行one-hot编码。

例如： 假设从我们的训练文档中抽取出100个唯一不重复的单词组成词汇表。我们对这100个单词进行one-hot编码，得到的每个单词都是一个100维的向量，向量每个维度的值只有0或者1，假如单词have在词汇表中的出现位置为第3个，那么have的one-hot表示就是一个第三维度取值为1，其他维都为0的100维的向量。

word2vec原理简述

写在前面

现在word2vec已经成为了自然语言处理领域的基础，在他之后的预训练模型或多或少都借鉴了他的一部分思想。

在word2vec训练完成之后，我们并不会使用这个模型处理新的任务，而是需要它的参数矩阵。word2vec模型有两种训练方法，skip-gram和CBOW。本文主要介绍使用skip-gram方法及其实现代码。

skip-gram

如下图所示，直观理解skip-gram是给定input word来预测上下文。

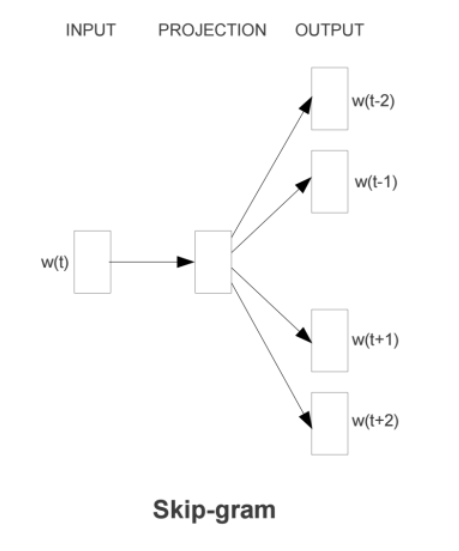
训练过程

我们拿“I have an apple”这句话举例。

1. 首先选一个中间词作为input word，例如我们选择了have。
2. 定义一个参数skip_windows ，它代表着从input word 的一侧（左或者右）选取词的数量，例如我们选取skip_windows = 2,那么获得的窗口中的词(包换input word)是[I,have,an,apple]
3. 定义一个参数num_skips ,他代表从整个窗口中选用多少次作为output word.例如当skip_windows =2,并且num_skips =2时，我们会得到两组{input word,output wold}。
4. 神经网络通过这些数据输出一个概率分布，这个概率代表着我们词典中每个词是output wold的可能性。

代码

网络结构定义代码

import math
import numpy as np
import paddle.fluid as fluid

def skip_gram_word2vec(dict_size, embedding_size, is_sparse=False, neg_num=5):
    datas = []
    input_word = fluid.layers.data(name="input_word", shape=[1], dtype='int64')
    true_word = fluid.layers.data(name='true_label', shape=[1], dtype='int64')
    neg_word = fluid.layers.data(
        name="neg_label", shape=[neg_num], dtype='int64')

    datas.append(input_word)
    datas.append(true_word)
    datas.append(neg_word)

    py_reader = fluid.layers.create_py_reader_by_data(
        capacity=64, feed_list=datas, name='py_reader', use_double_buffer=True)

    words = fluid.layers.read_file(py_reader)
    init_width = 0.5 / embedding_size
    input_emb = fluid.layers.embedding(
        input=words[0],
        is_sparse=is_sparse,
        size=[dict_size, embedding_size],
        param_attr=fluid.ParamAttr(
            name='emb',
            initializer=fluid.initializer.Uniform(-init_width, init_width)))

    true_emb_w = fluid.layers.embedding(
        input=words[1],
        is_sparse=is_sparse,
        size=[dict_size, embedding_size],
        param_attr=fluid.ParamAttr(
            name='emb_w', initializer=fluid.initializer.Constant(value=0.0)))

    true_emb_b = fluid.layers.embedding(
        input=words[1],
        is_sparse=is_sparse,
        size=[dict_size, 1],
        param_attr=fluid.ParamAttr(
            name='emb_b', initializer=fluid.initializer.Constant(value=0.0)))
    neg_word_reshape = fluid.layers.reshape(words[2], shape=[-1, 1])
    neg_word_reshape.stop_gradient = True

    neg_emb_w = fluid.layers.embedding(
        input=neg_word_reshape,
        is_sparse=is_sparse,
        size=[dict_size, embedding_size],
        param_attr=fluid.ParamAttr(
            name='emb_w', learning_rate=1.0))

    neg_emb_w_re = fluid.layers.reshape(
        neg_emb_w, shape=[-1, neg_num, embedding_size])
    neg_emb_b = fluid.layers.embedding(
        input=neg_word_reshape,
        is_sparse=is_sparse,
        size=[dict_size, 1],
        param_attr=fluid.ParamAttr(
            name='emb_b', learning_rate=1.0))

    neg_emb_b_vec = fluid.layers.reshape(neg_emb_b, shape=[-1, neg_num])
    true_logits = fluid.layers.elementwise_add(
        fluid.layers.reduce_sum(
            fluid.layers.elementwise_mul(input_emb, true_emb_w),
            dim=1,
            keep_dim=True),
        true_emb_b)
    input_emb_re = fluid.layers.reshape(
        input_emb, shape=[-1, 1, embedding_size])
    neg_matmul = fluid.layers.matmul(
        input_emb_re, neg_emb_w_re, transpose_y=True)
    neg_matmul_re = fluid.layers.reshape(neg_matmul, shape=[-1, neg_num])
    neg_logits = fluid.layers.elementwise_add(neg_matmul_re, neg_emb_b_vec)
    #nce loss

    label_ones = fluid.layers.fill_constant_batch_size_like(
        true_logits, shape=[-1, 1], value=1.0, dtype='float32')
    label_zeros = fluid.layers.fill_constant_batch_size_like(
        true_logits, shape=[-1, neg_num], value=0.0, dtype='float32')

    true_xent = fluid.layers.sigmoid_cross_entropy_with_logits(true_logits,
                                                               label_ones)
    neg_xent = fluid.layers.sigmoid_cross_entropy_with_logits(neg_logits,
                                                              label_zeros)
    cost = fluid.layers.elementwise_add(
        fluid.layers.reduce_sum(
            true_xent, dim=1),
        fluid.layers.reduce_sum(
            neg_xent, dim=1))
    avg_cost = fluid.layers.reduce_mean(cost)
    return avg_cost, py_reader

def infer_network(vocab_size, emb_size):
    analogy_a = fluid.layers.data(name="analogy_a", shape=[1], dtype='int64')
    analogy_b = fluid.layers.data(name="analogy_b", shape=[1], dtype='int64')
    analogy_c = fluid.layers.data(name="analogy_c", shape=[1], dtype='int64')
    all_label = fluid.layers.data(
        name="all_label",
        shape=[vocab_size, 1],
        dtype='int64',
        append_batch_size=False)
    emb_all_label = fluid.layers.embedding(
        input=all_label, size=[vocab_size, emb_size], param_attr="emb")

    emb_a = fluid.layers.embedding(
        input=analogy_a, size=[vocab_size, emb_size], param_attr="emb")
    emb_b = fluid.layers.embedding(
        input=analogy_b, size=[vocab_size, emb_size], param_attr="emb")
    emb_c = fluid.layers.embedding(
        input=analogy_c, size=[vocab_size, emb_size], param_attr="emb")
    target = fluid.layers.elementwise_add(
        fluid.layers.elementwise_sub(emb_b, emb_a), emb_c)
    emb_all_label_l2 = fluid.layers.l2_normalize(x=emb_all_label, axis=1)
    dist = fluid.layers.matmul(x=target, y=emb_all_label_l2, transpose_y=True)
    values, pred_idx = fluid.layers.topk(input=dist, k=4)
    return values, pred_idx

参考资料

[1] Rong X. word2vec parameter learning explained[J]. arXiv preprint arXiv:1411.2738, 2014.

[2] https://zhuanlan.zhihu.com/p/37471802

[3] https://aistudio.baidu.com/aistudio/projectdetail/978573